ARTICLES
Follow Us
Be the first to know
Armahn Existentialist Physics (AEP) : Axioms for Gravity
By:
Arman M Nazari
President,
Global Technical Resources | Aerospace & Defense SME


Axiom 1 – Gravity Appears when it is measured
AEP Causal Availability Principle
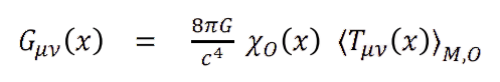
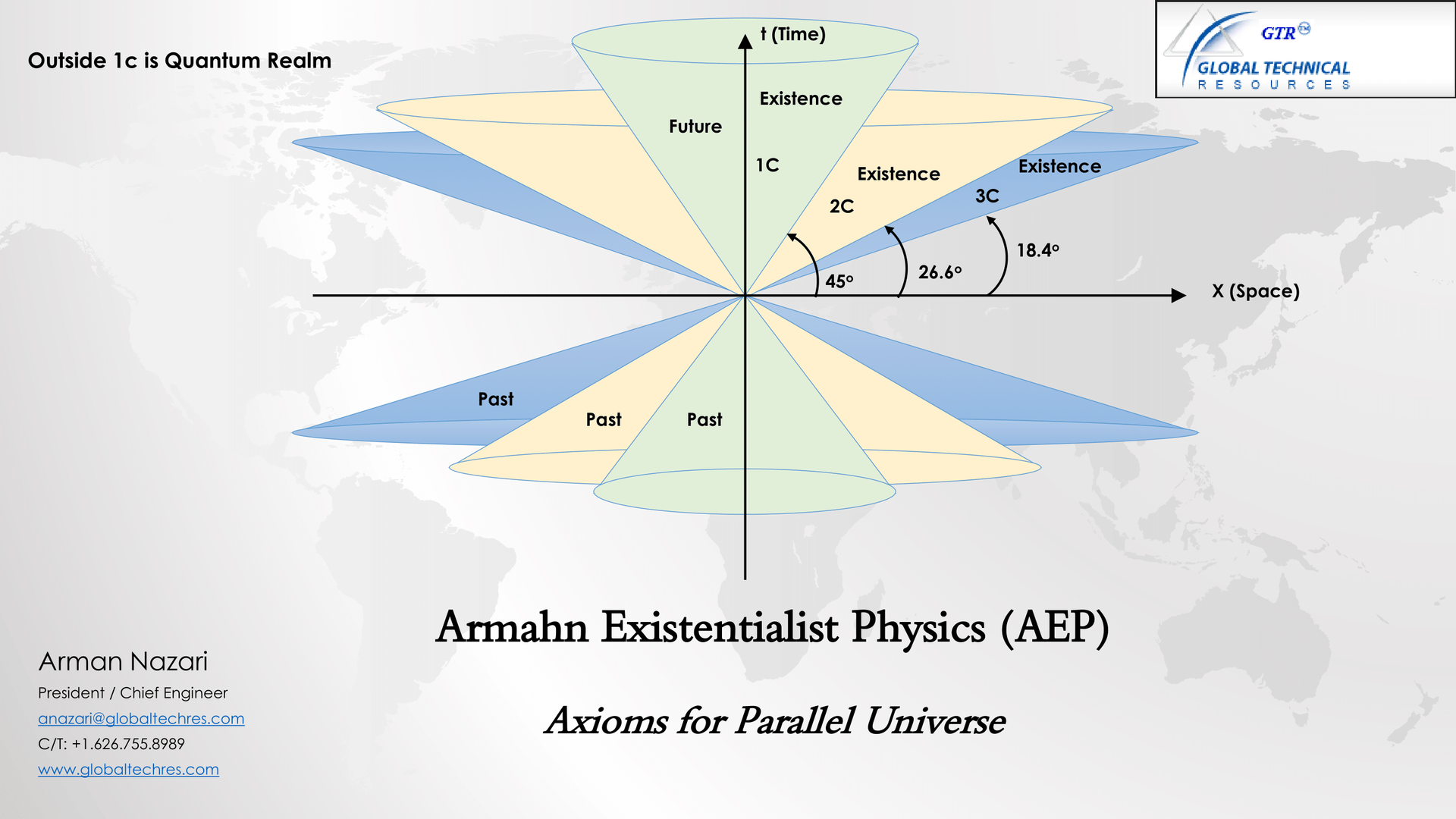
Axiom (Existential Light-Cone Bound):
Spacetime curvature (gravity) is realized only when stress–energy is measured within the causal light-cone of an observer 𝑂. 1. For matter-based observers (humanoid existence), the causal cone is bounded by the universal speed of light 𝑐.
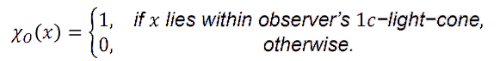
2. Other existential strata may possess cones bounded by higher critical speeds (2𝑐, 3𝑐, …). These do not alter the experienced physics of humanoid observers confined to the 1𝑐-cone but extend the framework of AEP to layered realities.
• We only feel gravity when we measure energy/matter inside our 1c light-cone.
• Higher-speed cones (2c, 3c, …) may exist in other existential domains, but our lived reality is bound by the 1𝑐-cone.
Gravity as Measurement:
Gravity does not exist as a continuous background field. Instead, it appears only when it is measured- that is, when matter (or energy) interacts with matter (or fields) in such a way that a relative force or curvature is registered.
Novelty of Axiom:
• Einstein’s view (GR): Gravity = geometry. It’s always there as curvature of spacetime, independent of whether you measure it.
• Newton’s view: Gravity = force at a distance. It acts continuously.
• Quantum mechanics view (forces in general): An interaction is registered only when exchange particles (gravitons, hypothetically) are absorbed/emitted.
• AEP statement: Gravity is not continuously present, rather collapses into existence when measured (like quantum wavefunctions do).
• Apple falling: the measurement is your hand or the ground feeling the impact.
• Walking: each step is a local “gravity measurement” by your body.
• Without measurement, gravity is just potential, not existence.
This really parallels the quantum measurement axiom but applies it to spacetime curvature itself. AEP is merging Einstein’s relativity (geometry) with Bohr’s “reality emerges when measured.”
Why this is powerful?
• It aligns with AEP’s light-cone view: gravity only manifests when information exchange crosses cones (when one system measures another).
• It reframes Einstein’s equivalence principle: instead of “you feel gravity as acceleration,” AEP proposes “you feel gravity only when measuring acceleration.”
• It could bridge to quantum gravity: gravitons don’t exist as a field everywhere, only in actual measurement interactions.
Conclusion:
Gravity is not a background field but an emergent effect of measurement.
Spacetime geometry is latent. When stress–energy is measured, the latent geometry is updated, i.e. gravity emerges for that observer. This update can be expressed mathematically as a “collapse” across the measurement surface, but physically it means: gravity only becomes real when measured.
More Interpretation:
• In Einstein’s relativity, gravity is always “on” as curvature.
• In AEP, gravity is latent until there is a measurement-like interaction.
• Measurement can be macroscopic (apple falling into a hand, a step pressing against the ground) or microscopic (field quanta registering curvature). • This parallels quantum mechanics: just as wavefunctions collapse upon measurement, spacetime curvature “collapses” into gravity when interactions occur.
Symbolic Form (proposal):
Let 𝐺𝜇𝜈denote Einstein’s curvature tensor, and 𝑀, a measurement operator acting on matter/field states.
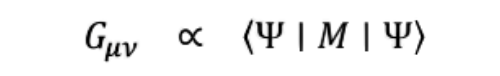
That is: curvature (gravity) is only realized when a measurement interaction takes place.
1. The Objects in AEP Equation
• 𝐺𝜇𝜈: In Einstein’s General Relativity, this is the Einstein curvature tensor, it encodes the curvature of spacetime caused by mass-energy.Normally it appears in Einstein’s field equation:
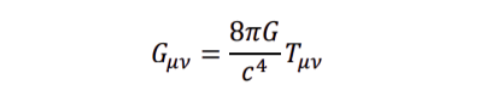
• where 𝑇𝜇𝜈is the stress-energy tensor (matter/energy content).
• 𝑀: AEP has introduced a measurement operator, this is drawn from Quantum Mechanics language. In QM, measurement is represented by operators acting on quantum states.
• Ψ ∣ 𝑀 ∣ Ψ : This is the expectation value of the measurement operator 𝑀, in the quantum state Ψ. It tells you the outcome (on average) when you measure 𝑀in state Ψ.
2. What AEP is Saying?
AEP replaces Einstein’s “always-on curvature” with a conditional one:
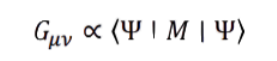
This means:
• Curvature (gravity) does not exist as a static background.
• Instead, it emerges only when a measurement (interaction) happens.
• Measurement here could mean:
• An apple hitting your hand.
• Earth’s surface resisting your step.
• Two masses disturbing each other’s spacetime.
So, the act of interaction = act of realizing curvature
3. The Two Ψ’s
• ∣Ψ⟩The initial state of matter/field.
• ⟨Ψ ∣ :The same state, but as a “bra” (mathematical dual) to make an inner product.
Together, Ψ ∣ 𝑀 ∣ Ψ is a scalar expectation value that says:
“How much of the measurement operator 𝑀, is realized in the state Ψ?”
4. Interpretation in AEP
• Einstein: curvature is always there, whether you measure it or not.
•
AEP: curvature = potential, but
gravity only appears when measurement/interaction collapses existence into a definite direction.
• In AEP symbolic form:
Curvature (existence disturbance)
← →
Measurement outcome of matter
Spacetime curvature (gravity) is not a permanent background structure, but the realized expectation of interactions. It only “shows up” when matter states interact in measurable ways.
Impact:
AEP Field Equation 1.0
“Curvature is realized only upon measurement.”
Start with Einstein’s equation:
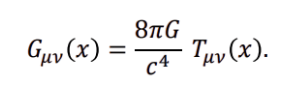
In
AEP, the right-hand side is not the always-on stress–energy.
Instead, it is the measured/realized stress–energy, conditioned on an interaction (measurement) by an observer/system 𝑂.
1) Replace 𝑇𝜇𝜈by a conditional expectation
* Let 𝜌 be the (possibly quantum) state of matter/fields and 𝑀𝑂 𝑥 a POVM/measurement operator localized near spacetime point 𝑥 for observer/system 𝑂. Define the measured stress–energy as:
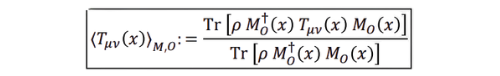
For projective measurements, take 𝑀𝑂 𝑥 = 𝑃𝑂 𝑥
Then the
AEP field equation is
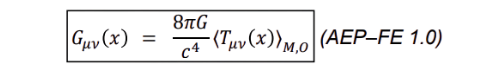
Meaning: spacetime curvature at 𝑥, is the curvature actually realized by the measurement/interaction 𝑀𝑂that occurs (or is accessible) there.
* For detail explanation see Appendix A
2) Causality / “light-cone availability”
The measurement must be causally available to the observer 𝑂. Encode this with a causal “window” 𝜒𝑂 𝑥 that is 1 only inside 𝑂’s light-cone (and while the apparatus is active):
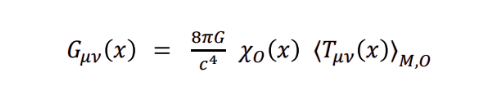
• 𝜒𝑂 𝑥 = 1 : the record can reach 𝑂⇒ gravity is realized/experienced.
• 𝜒𝑂 𝑥 = 0 : outside the light-cone or no measurement ⇒ no experienced gravity for 𝑂(only latent geometry)
3) Collapse / update across a measurement hypersurface
If a measurement occurs on a spacelike (or timelike) hypersurface Σ, the matter state updates
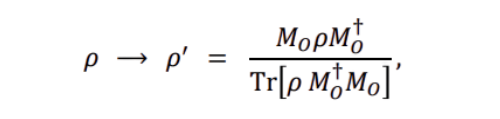
and the experienced geometry jumps accordingly:
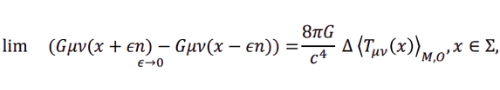
with 𝑛the normal to Σ. This encodes your statement: “spacetime collapses when gravity is measured.”
Step 4: "Define the measured stress-energy as:"
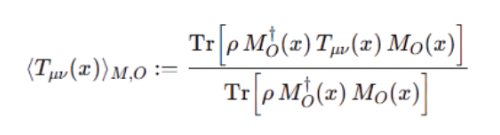
Let's unpack this:
• Tr = trace, the quantum way of averaging over states.
Numerator:
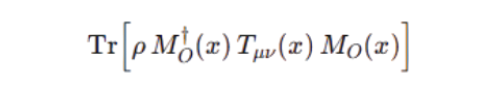
This means: take the stress-energy tensor Tμν, but sandwich it between the measurement operator and the system state.
→ This gives the measured contribution of stress-energy at point x.
•
Denominator:
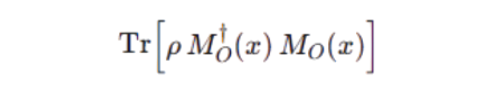
This is just the normalization: the probability that the measurement outcome actually happens.
So overall:
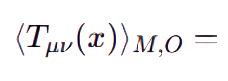
average stress-energy seen by measurement Mo at x.
Step 5: “Then the AEP field equation is …”
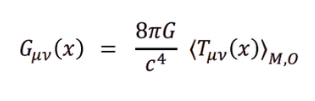
This is
AEP Field Equation 1.0.
Instead of saying
curvature = all energy, AEP is saying:
curvature = only the measured energy–momentum, relative to a measurement event.
Why this is powerful?
• It unifies relativity (geometry) with quantum mechanics (measurement).
• It implies gravity is not a universal background but an emergent phenomenon of relational measurement.
• It opens the door for describing gravity in terms of quantum information exchange between cones (your 1c, 2c, 3c layers).
AEP reframing gravity as not “always there” but “becoming real only when registered.”
Spacetime as Direction of Existence
1. Spacetime as Direction of Existence Spacetime
provides the direction of existence for matter and energy. This is why objects such as an apple “fall”, not because a continuous force is pulling them, but because the geometry of spacetime defines their natural path toward the center of Earth (or more generally, along geodesics).
2. Gravity as Emergent Force
Gravity as a force does not exist continuously. It only emerges when measured, that is, when one body interacts with another and a relative effect is registered (e.g., the apple striking the ground, or your foot pressing against Earth). In other words, gravity-as-curvature always defines possible motion, but gravity-as-force is experienced only upon measurement.
How this fits with known physics?
• Einstein’s GR → Gravity is always there as curvature, encoded in 𝐺𝜇𝜈.
• AEP refinement → Curvature gives a direction of existence, but the felt force of gravity only appears through measurement (unlike the collapse of a quantum state).
• Apple example:
• Path to Earth = dictated by existence (spacetime geometry).
• Feeling of weight, impact, or “force” = emerges when measured (contact interaction with Earth).
Symbolic Expression
We can split gravity into two layers:
1. Existence layer (geometric):
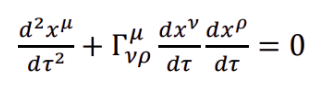
objects follow geodesics = direction of existence
2. Measurement layer (force):

where 𝑀, is a measurement operator (apple hitting the ground, step on Earth, a detector).
Gravity in AEP has two layers:
1. Existence layer (geometry):
Spacetime curvature defines possible directions of existence (geodesics). Objects “fall” along these paths, but without interaction, this is just latent.
2. Measurement layer (force):
Gravity becomes real when matter interacts with matter, e.g. when the apple hits the ground, when you feel your weight on Earth. At that instant, the measurement operator 𝑀turns geometry into an experienced force.
Einstein: gravity = geometry everywhere.
AEP: geometry is latent existence; gravity as a force only emerges in measurement.
APPENDIX A
Detail Explanation
Mathematics Background:
The expression:
⟨Ψ|𝑀|Ψ⟩
is a core concept in quantum mechanics that represents the expectation value of a physical quantity. This is the probabilistic weighted average of all possible outcomes if you were to measure that quantity for a system in a particular quantum state.
Here is a breakdown of the notation:
- Ψ⟩: This is a "ket" vector, and it represents the quantum state of a system. It can be thought of as a state vector in a complex vector space called a Hilbert space. In position space, the ket is related to the wavefunction, Ψ(x), but the ket itself is an abstract, representation-independent vector
- 𝑀: This is a Hermitian operator that corresponds to a measurable physical quantity, or observable, such as position, momentum, gravity, or energy. The operator acts on the state vector Ψ⟩.
- ⟨Ψ|𝑀|Ψ⟩: This entire expression denotes the inner product between the bra ⟨Ψ and the ket M|Ψ⟩. It produces a single, real number: the expectation value of the operator 𝑀, for a system in the state Ψ⟩.
Sequence:
Step 1: “Replace 𝑇𝜇𝜈 by a conditional expectation”
𝑇𝜇𝜈:
In Einstein’s relativity, this is the stress–energy tensor. It encodes matter, energy, momentum, pressure, etc. It’s the source of curvature (gravity). “Replace … by a conditional expectation”:
Instead of taking 𝑇𝜇𝜈 as something always present, we only take its value conditioned on a measurement. In other words: Only the part of energy–momentum that is actually registered by an interaction should count as sourcing curvature.
Step 2: “Let 𝜌be the (possibly quantum) state of matter/fields …”
- 𝜌: This is the state of the system. In quantum mechanics, 𝜌 is called a density matrix. It can describe pure states (like ∣ Ψ⟩) or mixed ensembles.
- “possibly quantum” : If we’re working classically, 𝜌 could just mean the distribution of matter. But in AEP we allow quantum uncertainty.
Step 3: {M_O(x)} — a POVM/measurement operator localized near spacetime point x for observer/system O.
- M_O(x):
- This is the measurement operator — it encodes what kind of measurement/interactions the observer/system O can perform at spacetime point x.
- (POVM = Positive Operator-Valued Measure, a general formalism for quantum measurements.)
- “localized near spacetime point x”:
- The measurement only makes sense at the place and time where the interaction happens.
- “for observer/system O”:
- Measurements are relative — what you see depends on who/what is doing the observing.
Step 4: Define the measured stress–energy as:
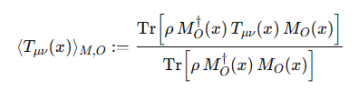
Let's unpack this:
- Tr = trace, the quantum way of averaging over states.
- Numerator:
This means: Take the stress–energy tensor TμνT_{\mu\nu}, but sandwich it between the measurement operator and the system state. → This gives the measured contribution of stress–energy at point xx.
- Denominator:
This is just the
normalization: The probability that the measurement outcome actually happens.
So overall:
average stress–energy seen by measurement MO at x.
Step 5: “Then the AEP field equation is …”
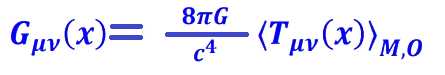
This is AEP Field Equation 1.0.
Instead of saying
curvature = all energy, you’re saying:
curvature = only the measured energy–momentum, relative to a measurement event.
Einstein (GR view):
- Matter and energy always curve spacetime.
- The stress–energy tensor Tμν is the source of curvature GμνG.
- Gravity is “always on,” even if no one measures it.
AEP:
- Matter and energy are latent sources of gravity.
- They do not generate realized curvature unless there is an interaction/measurement.
- Gravity (curvature) emerges only when matter or energy is registered by a measurement — for example, when the apple hits your hand, or when your foot presses on the ground.
In AEP, matter and energy exist as latent potentials. Gravity (the curvature of spacetime) is not continuously present as in Einstein’s GR, but is realized only when those potentials are measured through interaction. Measurement is what turns latent matter/energy into active spacetime curvature.
AEP Causal Availability Principle (refined): Spacetime curvature (gravity) is realized only when stress–energy is measured within the causal light-cone of the observer.
- For matter-based (humanoid) observers, this cone is bounded by c.
- Higher or parallel existential frames may be bounded by
2c, 3c, ..., but these do not alter the effective laws in the
1c-cone of our existence.
Title: Causality / “light-cone availability”
- Causality: In relativity, “cause precedes effect”; nothing can influence you faster than the speed of light.
- Light-cone availability:
The light-cone is the region of spacetime that light (or any signal ≤ c) can reach. “Availability” means: can the information about the measurement actually get to the observer?
Sentence: “The measurement must be causally available to the observer O.”
- Measurement must be causally available: Even if some matter/energy exists far away, you can only count it as realized gravity for you if the information about it can reach you without breaking causality. Example: A star explodes in another galaxy. Its gravity for you is not realized until the disturbance enters your light-cone.
Sentence:
“Encode this with a causal ‘window’ χ0(x)\chi_0(x), that is 1 only inside 0’s light-cone (and while the apparatus is active).”
Encode this:
We put this rule into math.
Causal window
χ0(x)\chi_0(x):
A function that switches between ON (1) and OFF (0).
- χ0(x)=1\chi_0(x) = 1: the event at spacetime point x can affect observer 0.
- χ0(x)=0\chi_0(x) = 0: it cannot.
Only inside 0’s light-cone:
If the event is in your past light-cone (or future interaction region), it can causally affect you.
Apparatus active:
Even if causally allowed, no measurement = no realized gravity.
Equation:
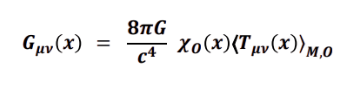
- G_{μν}(x): Curvature (gravity) at point x
- (8πG / c⁴): Einstein’s proportionality constant
- χ₀(x): The causal switch
- ⟨T_{μν}(x)⟩_{M,0}: Measured stress-energy relative to observer 0
Bullets:
So: Gravity = measured stress–energy × causal availability.
1.x₀(x) = 1
- The record can reach observer O.
- Gravity is realized/experienced.
- Example: You feel the apple when it hits your head, because that measurement is inside your light-cone.
2.x₀(x) = 0
- Outside your light-cone, or no measurement happened.
- You have no experienced gravity from it.
- The geometry is only latent (it exists in principle, but you don’t feel it yet).
- Example: A galaxy 1 billion light-years away collapsing right now doesn’t affect your gravity yet — you’ll only experience it when the light/gravitational waves arrive.
Connection to Lorentz causality:
- The Lorentz transformation ensures that the speed of light is the ultimate speed limit.
- In standard relativity: causality = signals can’t outrun c.
- In AEP: This is built into the equation by multiplying with x₀(x).
- If an event is outside your light-cone (superluminal), x₀ = 0.
- If it is inside, x₀ = 1.
Lorentz transformations define the light-cone, and AEP uses x₀(x) to enforce that only causally-allowed measurements create realized gravity for you.
In AEP, gravity isn’t global and automatic. You only feel gravity from things whose influence can physically reach you (inside your light-cone) and that you measure through interaction. If it’s too far away or too fast (outside your light-cone), it stays latent until it becomes causally available.
- The existential light-cone for human (or matter-based) observers is bound by c (the usual speed of light).
- That’s why we only register causal signals at c.
- Other regimes (e.g. higher-order structures, parallel universes, or different existential strata) may have cones bounded by 2c, 3c, ...
- This does not violate relativity as experienced by us, because our measurements are confined to the c-bound cone.
This way AEP preserves:
- Consistency with Einstein (no superluminal influence inside our cone).
- Openness for AEP (multiple speeds of light in different existential layers).
3rd Title: "Collapse / update across a measurement hypersurface"
- Collapse:
Borrowed from quantum mechanics (wavefunction collapse). It means the state “jumps” when you measure. - Update:
More general than collapse — includes any state change when new information is registered. - Hypersurface:
A 3D slice of 4D spacetime. For example: • Spacelike hypersurface = “all space at one moment of time.” • Timelike hypersurface = “a worldtube where measurements occur continuously in time.”
If a measurement happens anywhere across such a slice, it updates the state of matter and geometry.
Equation 1: State update
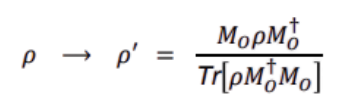
Quantum Measurement Update Rule
- ρ:
The quantum state (density matrix) of matter/fields before measurement.
- ρ′:
The new state after measurement.
- M₀:
The measurement operator corresponding to observer 0.
- M₀†:
Hermitian conjugate of M₀ — ensures probabilities remain real and consistent.
- Fractional structure:
Numerator: Apply the measurement operator to the old state.
Denominator: Normalize it (so probabilities sum to 1).
This is the standard quantum measurement update rule — the state “collapses” or “updates” when you measure.
Text: “and the experienced geometry jumps accordingly” → Not just the matter state changes — the geometry itself (gravity) also “collapses” when a measurement happens.
Equation 2: Geometry jump condition
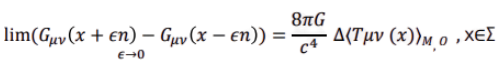
- G_{μν}: Einstein curvature tensor (spacetime geometry, i.e. gravity)
- lim_{ε → 0}: We’re looking at the instantaneous jump in curvature across the hypersurface Σ
- x + ε: Just after the hypersurface, moving a tiny step in the normal direction
- x − ε: Just before the hypersurface
- Subtraction: The difference in geometry across the measurement event
- RHS: (8π / c⁴) — standard Einstein factor
- ΔT_{μν}(x): The measured change in stress-energy due to the measurement
- n: The vector normal to Σ — tells you the direction of comparison (“before” vs “after”)
When a measurement happens, the geometry (curvature) jumps in proportion to the change in measured stress-energy.
with n the normal to Σ
- n: The vector perpendicular to the hypersurface Σ
- It simply tells you the direction we’re comparing — “before” vs “after”
Final text:
This encodes AEP statement: “spacetime collapses when gravity is measured.”
- Before measurement: latent geometry
- After measurement: realized geometry
- The jump condition formalizes how gravity itself undergoes a discontinuous update, just like a quantum wavefunction
When you measure matter/energy across some slice of spacetime, you don’t just change your knowledge — you change the actual experienced geometry. Gravity itself “collapses” across that surface, updating to reflect the measured stress-energy.
Spacetime geometry is latent. When stress-energy is measured, the latent geometry is updated — i.e., gravity emerges for that observer. This update can be expressed mathematically as a “collapse” across the measurement surface, but physically it means gravity only becomes real when measured.
- AEP keeps “gravity emerges when measured” as a central AEP axiom
- AEP uses “collapse” only as a mathematical analogy to describe the update rule (since physicists are used to the word from quantum theory)
1. Existence layer (geometric):
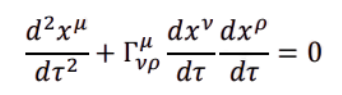
- This is the geodesic equation from general relativity
- x^μ: the spacetime position of an object
- τ: proper time along its worldline
- Γ^μ_{ρν}: Christoffel symbols — encode how spacetime is curved
“Objects move along geodesics, the natural straightest possible paths in curved spacetime.”
- In AEP language: this is the “direction of existence” — it tells matter where to go if left alone, without measuring it
Gravity is not yet a force — it’s just the structure of spacetime telling matter how to exist
2. Measurement layer (force):
F^μ_gravity = M(curvature matter state)
- F^μ_gravity: the actual force-like experience of gravity
- M: the measurement operator — represents when matter interacts (apple hits ground, your feet step, a detector reads it)
“Gravity as a force only emerges when curvature interacts with matter through measurement.”
- If no measurement → only latent geometry
- If measurement occurs → the “force” of gravity is experienced